Learning-Based Distributed Spatio-Temporal 𝑘 Nearest Neighbors Join

Download paper here

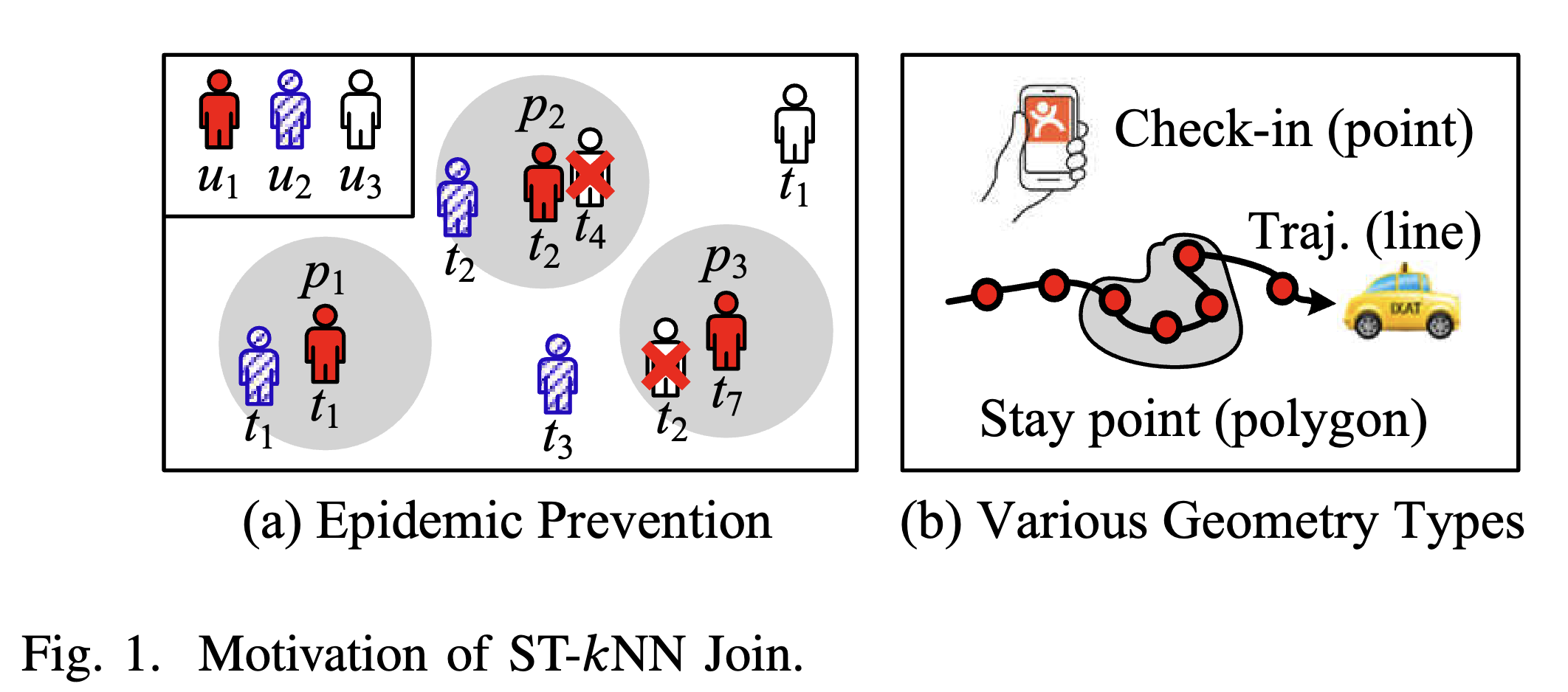
Abstract: The rapid development of positioning technology produces an extremely large volume of spatio-temporal data with various geometry types such as point, line string, polygon, or a mixed combination of them. As one of the most fundamental but time-consuming operations, 𝑘 nearest neighbors join (𝑘NN join) has attracted much attention. However, most existing works for 𝑘NN join either ignore temporal information or consider only point data. Besides, most of them do not automatically adapt to the different features of spatio-temporal data.

This paper proposes to address a novel and useful problem, i.e., ST-𝑘NN join, which considers both spatial closeness and temporal concurrency. To support ST-𝑘NN join over a large amount of spatio-temporal data with any geometry types efficiently, we propose a novel distributed solution based on Apache Spark. Specifically, our method adopts a two-round join framework. In the first round join, we propose a new spatio-temporal partitioning method that achieves spatio-temporal locality and load balance at the same time. We also propose a lightweight index structure, i.e., Time Range Count Index (TRC-index), to enable efficient ST-𝑘NN join. In the second round join, to reduce the data transmission among different machines, we remove duplicates based on spatio-temporal reference points before shuffling local results. Furthermore, we design a set of models based on Bayesian optimization to automatically determine the values for the introduced parameters. Extensive experiments are conducted using three real big datasets, showing that our method is much more scalable and achieves 9X faster than baselines, and that the proposed models can always predict appropriate parameters for different datasets. The source codes are released at https://github.com/Spatio-Temporal-Lab/stknnjoin.

Li, R., Li, J., Zhou, M., Wang, R., He, H., Chen, C., … & Zheng, Y. (2024). Learning-Based Distributed Spatio-Temporal $k$ Nearest Neighbors Join. IEEE Transactions on Big Data.