多维反向k近邻查询
Published:
近十年来,空间点数据的反向k最近邻(R$k$NN)查询引起了研究者的广泛关注。给定一个数据点 q,反向k最近邻(R$k$NN)查询查找每一条将q当作它的k个近邻之一的数据点。由于q与这些数据点很接近,所以q对这些点的影响很大。例如,居民有极大的可能会去最近的k个商店购物。因此,在市场调研中,可以通过检索所有将这家商店当作k 个最近邻之一的居民点,来评估一家新开的便利店q潜在的客户。R$k$NN还可在更多的商业选址场景中使用,具有很重要的现实意义和实用价值。在本文中,提供一种设施或服务的对象(如购物市场、加油站)称为设施,使用该设施的对象(如居民、司机)称为用户。在这个上下文中,给定一个查询设施q, 其R$k$NN返回所有将q作为k个最接近的设施之一的用户。本文将基于这种上下文介绍四种R$k$NN算法, 即six regions 、TPL、FINCH、InfZone。
[本文总阅读量: 次]
简介
近十年来,空间点数据的反向k最近邻(R$k$NN)查询引起了研究者的广泛关注。给定一个数据点 q,反向k最近邻(R$k$NN)查询查找每一条将q当作它的k个近邻之一的数据点。由于q与这些数据点很接近,所以q对这些点的影响很大。例如,居民有极大的可能会去最近的k个商店购物。因此,在市场调研中,可以通过检索所有将这家商店当作k 个最近邻之一的居民点,来评估一家新开的便利店q潜在的客户。R$k$NN还可在更多的商业选址场景中使用,具有很重要的现实意义和实用价值。在本文中,提供一种设施或服务的对象(如购物市场、加油站)称为设施,使用该设施的对象(如居民、司机)称为用户。在这个上下文中,给定一个查询设施q, 其R$k$NN返回所有将q作为k个最接近的设施之一的用户。本文将基于这种上下文介绍四种R$k$NN算法, 即six regions 、TPL、FINCH、InfZone。
注:本文大多数算法描述参考于[7],更多R$k$NN算法和细节请参考原文。
基本定义和步骤
R$k$NN查询分为双色R$k$NN查询和单色R$k$NN查询。
双色R$k$NN查询:存在一个设施集F、一个用户集U。给定一个查询设施q(不一定在F中),一个双色R$k$NN查询返回每个用户$u\in U$,对于这些用户$u, q$是{$q\cup F$}中离它最近的k个设施之一。
单色R$k$NN查询:给定一组设施F和一个查询设施q(不一定在F中),一个单色R$k$NN查询返回每个设施$f\in F$,其中q是{$q\cup F−f$}中离它k个最近的设施之一。
在本文中,我们关注的是在欧氏空间中回答R$k$NN查询。由于R$k$NN查询的大部分应用是基于位置的服务,几乎所有现有的技术(如six regions [3]、TPL[4,5]、FINCH[6]、InfZone[1]等)都集中在二维位置数据上。因此,我们重点介绍在二维数据集上的算法。此外,双色R$k$NN查询在实际场景中有更多的应用程序。因此,本文主要焦点是双色查询。所有这些算法都假设数据集被R-tree或其变体(如R*-tree)进行索引。因此,接下来的介绍中,我们还假设设施和用户数据集都由两个R*树进行索引。
假设$dist(a, b)$表示两个对象的欧式距离。对于一个用户p, 如果存在至少k个设施F’, 对于任意f $\in $ F’, p到f的距离比q小,即$dist(p, f) < dist(p, q)$,则用户p不可能是q的R$k$NN之一,因为q不可能是p的kNN。
由于数据集的数量可能十分庞大,通过遍历所有用户并判断其是否满足条件,这是十分耗时且不合理的操作。前文提到,数据集会被R*-tree索引,每个R*-tree节点包含了大量的数据。因此,可通过先剪枝不合适的R*-tree实体(一个节点或一条数据),来减少查询开销。如果一个用户R*-tree实体$e$与至少k个设施(不包含q)的距离小于$q$,那么$e$可以被剪枝,因为e中包含的所有数据都具有至少k个比q近的设施。因此它们不可能是q的RkNN。
每个算法都可以分成两个步骤:
Filtering: 过滤阶段,每个算法使用一组设施来过滤不包含R$k$NN的搜索空间。由于使用所有数据的可能非常昂贵,算法首先会挑选一些设施来过滤搜索空间。这些设施称为过滤设施,包含这些设施的集合称为过滤集(表示为$S_{fil}$)。
**Verification: **验证阶段,检索不能使用$S_{fil}$过滤的用户,它们是可能的R$k$NN,称为候选用户。然后通过确认它是否是R$k$NN来验证每个候选用户。
算法
(1) Six-regions
Filtering: Stanoi等人[3]提出了一种基于Six-regions(6个区域)的方法,将以查询q为中心的整个空间划分为6个相等的区域,每个区域60$^{\circ}$,(下图中的P1到P6)。每个区域中,q的第k个最接近的设施定义了可以过滤的区域。换句话说,假设$d_i^k$是区域$P_i$中q与其第k个最近的设施之间的距离。那么任何在$P_i$中并且距离q大于$d_i^k$的用户u都不能是q的R$k$NN。
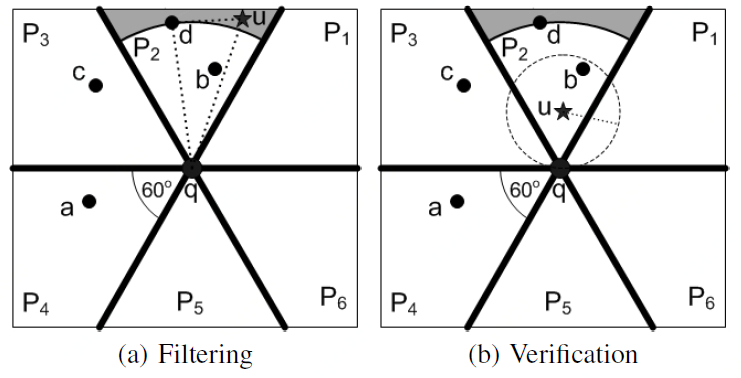
上图中展示了一个RkNN (k = 2)查询,设施包含q和四个编号从a到d的设施。在区域$P_2$中,d是距离q第二近的设施,则阴影区域可以被过滤,即$P_2$区域中只有位于白色区域的用户可以是R$k$NN。处于阴影区域的用户u不能是R$k$NN,因为它肯定更接近b和d,则所有u的kNN(k=2)不可能包含$q$。可以用三角形证明处于阴影部分的用户必然远离$q$。例如,对于设施d和用户u,可形成△qdu(如图(a))。因为$\angle dqu \le 60^{\circ}$ , 并且 $\angle qdu \ge 60^{\circ}$, 则 $dist(u,d) \le dist(u,q)$(大角对大边)。
Verification: 如前所述,位于分区$P_i$中的用户u,如果$dist(u,q) > d_i^k$,则$u$不能是$q$的R$k$NN 。在验证阶段,通过访问用户R*-tree来检索候选用户,并过滤mindist(e, q) >$d_i^k$的节点, 并通过Filtering步骤过滤$dist(u,q) > d_i^k$的用户,得到候选用户。然后每个候选用户通过一个布尔范围query来验证是否是q的R$k$NN。布尔查询以u为中心,半径为$dist(u, q)$作圆。当且仅当在以u为中心的圆中只有小于k个设施时,返回true,$u$是$q$的R$k$NN。如图(b)所示,以$u$为圆心,半径为$dist(u,q)$的圆,只包含两个设施。因此$u$为$q$的R$k$NN(k=2)。
(2) TPL
Filtering: Tao等人[4,5]提出的TPL可以说是R$k$NN查询中最流行的算法。他们首次将半空间剪枝的概念用于R$k$NN查询,并激发了许多后续工作。给定一个设施f和一个查询q, f和q之间的一条垂直平分线$B_{f:q}$ 将空间分成两半。设$H_{f:q}$表示包含f的半空间,$H_{q:f}$表示包含q的半空间,位于$H_{f:q}$中的每个点p,都满足$dist(p, f) < dist(p, q)$,也就是说,f可以裁剪位于$H_{f:q}$中的每个点p。
考虑下图(a)的例子,其中包含了一个查询q和四个设施(a到d)。因为p位于$H_{a:q}$中,因此,$dist(p, a) < dist(p, q)$,所以点p可以被设施a裁剪。请注意,被至少k个半空间裁剪的点p才不能是q的R$k$NN,才可以被过滤。如下图,假设k = 2,点p可以被过滤,因为它会被$H_{a:q}$和$H_{c:q}$裁剪。
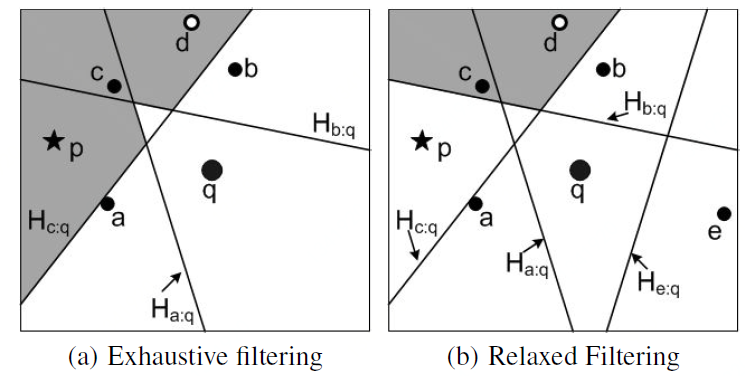
TPL的过滤算法从根节点开始访问设施R*-tree的节点,并将它们按与q的最小距离升序排列放入堆中。迭代地访问堆,如果一个被访问的实体e(可以是一个节点或者一个设施)可以被过滤(例如,e被至少k个设施裁剪),它将被忽略。否则,如果e是中间节点或叶节点,则将其子节点插入堆中。另一方面,如果e是一个设施,且无法裁剪,则将其插入过滤集$S_{fil}$中,其半空间用于过滤搜索空间。当堆为空时,过滤算法终止。在图(a)中,假设过滤算法以$b、c、a、d$的顺序迭代访问设施,当访问设施$b、c、a$时(即$S_{fil}= {b, c, a}$),过滤区域由半空间$H_{b:q}, H_{c:q}, H_{a:q}$的交集组成。如果k = 2,则阴影区域可以被过滤,因为其中的每个点都位于至少两个半空间中。如,当访问设施d时,可以使用筛选集对它进行剪枝。因此,在$S_{fil}$中不用插入d。
上面提到,TPL中的一个重要操作是确定设施实体是否可以使用一组过滤设施$S_{fil}$进行过滤。一种穷举的过滤策略如下:
设$S_{fil}$为包含m≥k个设施的过滤集,${f_1,…,f_k)}$为$S_{fil}$任意一个包含$k$个设施的子集。它们形成的过滤空间为 $\cap_{i=1}^{k} H_{f_i:q}$,每一个出现在这个空间中的点将被过滤。穷举过滤策略枚举每个这样的子集,并检查是否可以使用这些子集过滤R*-tree的节点。但是,这样的子集数量($C_m^{k}$)可能会很大。因此,TPL在过滤能力上做出了妥协,使用了以下成本较低的过滤策略(以下称为宽松过滤策略)。
首先,TPL根据希尔伯特值(Hilbert)对$S_{fil}$中设施按其空间位置进行排序。设排序后的顺序为$S_{fil} ={f_1,…,f_m)}$。然后,宽松过滤策略将其分成$m$个子集,分别为:${f_1,…,f_k)}$,${f_2,…,f{k+1})}$,…,${f_m,…,f{k-1})}$。总过滤成本为$O(km)$,因为要考虑m个子集,每个子集包含k个设施。如图(a), 假设$S_{fil} ={a,b,c}$。宽松过滤策略生成三个子集 ${a,b}$ 、${b,c}$和${c,a}$,并可过滤与穷举滤波相同的区域(即阴影区域)。这是因为在这种情况下,最大可能子集的个数等于m,即$C_{3}^{2} =3=m$。但是,在$S_{fil}$中添加一个新设施可能会减少过滤的面积,并且在添加该设施之前可以过滤的点可能不会再被过滤。假设设施e被插入,排序后的$S_{fil}$为${a, b, c, e}$。宽松过滤算法使用${a, b}, {b, c}, {c, e}和{e, a}$对搜索空间进行过滤。上图(b)展示了可以使用这些子集过滤的阴影区域。注意,经过过滤的区域已经变小,导致点p不能再被过滤。
为了更好地过滤节点e(节点或数据点),TPL使用一种名为kTrim的算法。对于包含k个连续设施的$S_{fil}$的子集,该算法裁剪掉节点中可以被这个子集过滤的部分。kTrim使用每个子集(共m个)迭代地修剪节点。在任何阶段,如果整个节点被裁剪,节点或数据点就可以被过滤,算法就会停止。
Verification: TPL迭代地访问用户R*-tree的节点,并使用$S_{fil}$对它们进行过滤。无法筛选的用户被插入到候选集中。与六个区域不同,TPL不会使用布尔范围查询来验证候选区域。取而代之地,TPL使用了一种更聪明的策略,它要求R*-tree的每个节点最多访问一次。具体地说,在过滤阶段遇到的设施R*-tree的节点和数据点保持在集合P中,验证算法轮询运行。在每一轮中,P中的一个节点被取出,并将其子节点被插入到P中。选择被取出的节点是基于它可以验证多少个候选节点。在每一轮中,利用P中的节点和数据点来识别可以用P验证的候选项,即可以确认为R$k$NN或保证不为R$k$NN。这样的候选项将被验证并从候选者集中删除。当候选集为空时,算法停止。
(3) FINCH
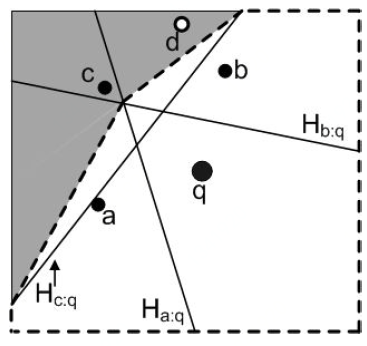
Filtering: Wu等人提出了一种名为FINCH的算法[6],旨在通过使用一种更方便的过滤策略来改进TPL。具体来说,它不使用子集来过滤节点,而是使用一个包围不能被过滤区域的凸多边形。多边形之外的任何条目都可以被过滤。考虑图(a)的例子,其中白色区域是非过滤的区域。FINCH用一个凸多边形来近似这个区域(参见下图中的白色区域,边界用虚线表示)。任何在这个多边形之外的节点都可以被过滤,也就是阴影部分。
凸多边形的计算成本较高,并且,每当一个新的设施添加到$S_{fil}$,它需要$O(m^2)$的时间开销来计算凸多边形,其中$m$是过滤集$S_{fil}$中设施的数量。然而,FINCH的过滤比TPL更有效,因为判断一个点是否包含在凸多边形里,可以在对数$O(log ~m)$时间内完成。因此,可以在$O(log ~m)$内过滤一个点。过滤一个节点需要$O(m)$,因为它可能需要计算矩形与凸多边形的交点。
Verification: 识别凸多边形内的用户并将其插入到候选集中。与6区域方法类似,每个候选用户都需要使用布尔范围查询进行验证。
(4) InfZone
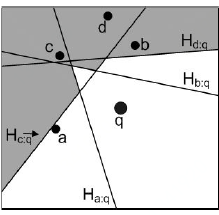
Filtering: Cheema等人[1,2]提出InfZone算法,利用影响区域的概念来改善验证阶段。影响区域是指当且仅当p位于该区域内时,点p为q的R$k$NN的区域。一旦计算了影响区域,就可以通过定位位于影响区域内的用户来回答R$k$NN查询。一种方法建立影响区的方法是绘制所有设施的半空间,被小于k个设施过滤的区域对应于影响区。例如,在下图中,q和所有设施之间的半空间被绘制为$Ha:q, Hb:q, Hc:q,和Hd:q$, 则阴影区域是过滤区域,白色区域是影响区域。回想一下,FINCH和TPL没有考虑$Hd:q$,因为当访问d时,会发现它位于过滤区域,因此会被忽略。作者提出了几个性质,以减少必须考虑的设施的数量,以正确计算合适的影响区域。该算法首先初始化影响区域为整个数据空间(矩形)。每当访问设施f时,其半空间$Hf:q$用于更新影响区,例如,通过删除至少k个设施修剪的部分。对于当前影响区域的每个顶点v,如果$minDist(e,v) > dist(v,q)$, 则不需要这个实体e(一个节点或一个设施)计算影响区域。因此,该算法只考虑不满足该条件的实体。请注意,检查是否需要设施实体需要$O(m)$,因为遍历影响区域的顶点数为$O(m)$。当在$S_{fil}$中插入新设施时,更新影响区域需要$O(m^2)$,其中m是$S_{fil}$中的设施总数。在它的扩展版[2]中,该成本优化到了$O(km)$。
Verification: 根据影响区域的定义,当且仅当p在影响区域内时,点p为R$k$NN。因此,算法将迭代访问用户R*-tree的实体,并忽略不与影响区域重叠的实体。位于影响区域内的用户则为R$k$NN。结果表明,影响区域为星形多边形,点包含在星形多边形边数可以在对数时间内完成,即验证用户的成本为$O(log~ m)$。为了过滤一个用户节点(即一个矩形),需要判断矩形是否与影响区相交,它花费$O(m)$。为了加快检查某个实体(节点或点)是否与影响区域重叠,InfZone被近似为两个圆:一个完全包含影响区域,另一个完全包含它(所有影响区域)。首先对照这些圆检查每个实体的重叠部分,以确定是否与影响区重叠。
复杂度分析:
| 过滤方法 | six-regions | TPL | FINCH | InfZone |
|---|---|---|---|---|
| 筛选设施节点 | O(1) | O(km) | O(m) | O(m) |
| 筛选设施数据点 | O(1) | O(km) | O(log m) | O(m) |
| 在$S_{fil}$中增加一个新设施 | O(log k) | O(log m) | O($m^2$) | O($m^2$) |
| 验证方法 | six-regions | TPL | FINCH | InfZone | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 过滤用户节点 | O(1) | O(km) | O(m) | O(m) | ||||||||||||
| 过滤用户点 | O(1) | O(km) | O(log m) | O(log m) | ||||||||||||
| 验证一个候选用户 | 布尔范围查询 | 范围查询 | 布尔范围查询 | O(log m) | ||||||||||||
| 预期候选人人数 | $\frac{6k | U | }{F}$ | $\frac{k | U | }{F}$ 至 $\frac{6k | U | }{F}$ | $\frac{k | U | }{F}$ 至 $\frac{6k | U | }{F}$ | $\frac{k | U | }{F}$ |
参考文献:
[1] M. A. Cheema, X. Lin, W. Zhang, and Y. Zhang. Influence zone: Efficiently processing reverse k nearest neighbors queries. In ICDE, pages 577–588, 2011.
[2] M. A. Cheema, W. Zhang, X. Lin, and Y. Zhang. Efficiently processing snapshot and continuous reverse k nearest neighbors queries. VLDB J., 21(5):703–728, 2012.
[3] I. Stanoi, D. Agrawal, and A. E. Abbadi. Reverse nearest neighbor queries for dynamic databases. In ACM SIGMOD Workshop, pages 44–53, 2000.
[4] Y. Tao, D. Papadias, and X. Lian. Reverse knn search in arbitrary dimensionality. PVLDB, pages 744–755, 2004.
[5] Y. Tao, D. Papadias, X. Lian, and X. Xiao. Multidimensional reverse k nn search. VLDB J., 16(3):293–316, 2007.
[6] W. Wu, F. Yang, C. Y. Chan, and K.-L. Tan. Finch: Evaluating reverse k-nearest-neighbor queries on location data. PVLDB, 1(1):1056–1067, 2008.
[7] Yang, S., Cheema, M. A., Lin, X., & Wang, W. (2015). Reverse k nearest neighbors query processing: experiments and analysis. PVLDB, 8(5), 605-616.
